写在开篇
二分模板一共有两个,分别适用于不同情况。
满足某个条件的第一个数
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时,其更新操作是r = mid或者l = mid + 1;,计算mid时不需要加1。1
2
3
4
5
6
7
8
9
10int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
满足某个条件的最后一个数
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时,其更新操作是r = mid - 1或者l = mid;,此时为了防止死循环,计算mid时需要加1。1
2
3
4
5
6
7
8
9
10int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
当我们将区间[l, r]划分成[r, mid - 1]和[mid, r]时,其更新操作是r = mid - 1或l = mid,此时为防止死循环,计算mid时需要+1,即:
选择
二分只有上述两种情况:
- 找大于等于给定数的第一个数
- 找小于等于给定数的最后一个数
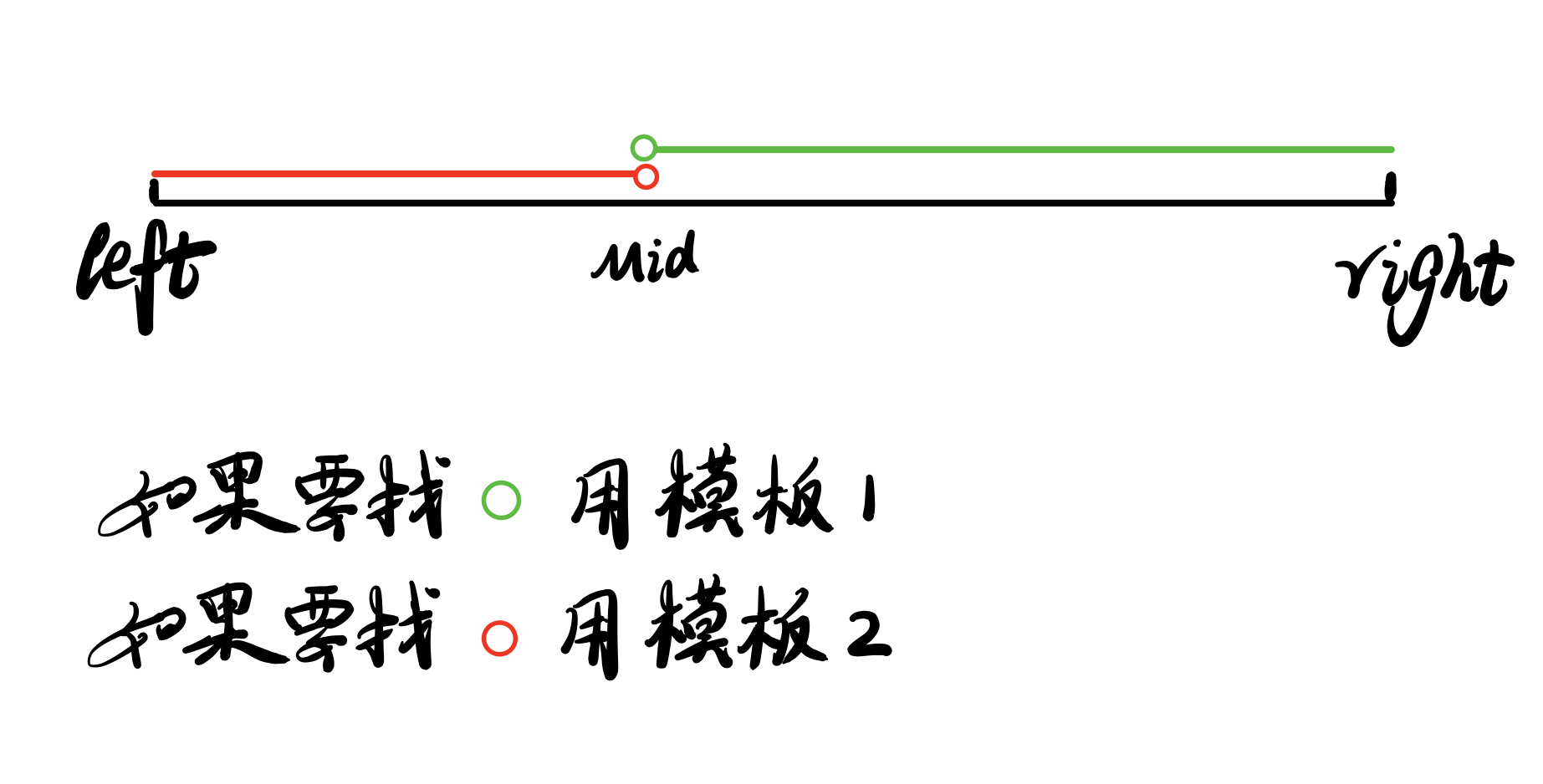 二分查找02
二分查找02
下面给一个对比的例子(leetcode34):
Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
Follow up: Could you write an algorithm with O(log n) runtime complexity?
1 | Example 1: |
思路:分别找出第一次出现的位置和最后一次出现的位置,即分别对应模板1和模板2。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public int[] searchRange(int[] nums, int target) {
if (nums == null || nums.length == 0) return new int[] {-1, -1};
int l = 0, r = nums.length - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target)
r = mid;
else
l = mid + 1;
}
if (nums[l] != target) return new int[] {-1, -1};
int start = l;
l = 0;
r = nums.length - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (nums[mid] <= target)
l = mid;
else
r = mid - 1;
}
int end = r;
return new int[] {start, end};
}
}
巨人的肩膀:
- acwing.com
